Introduction to Probability

Health Insurance, Poker, Investing, Blackjack and Lottery. What do these things among many others have in common? Yup you guessed it right, Probability.

Probability is the science of estimating likelihood of something happening. The likelihood of getting a heads on coin. The likelihood of a stock going up. The likelihood of you winning the lottery.

Understanding probability well is the most important skill that you can have in the area of statistics, data science and machine learning. Everything in this domain either is directly based on or at least touches Probability in some tangential way.

Mathematically speaking, Probability of anything occurring is the ratio of number of ways that particular thing can occur and number of all the possibilities.

$$ P(\text{Event}) = \frac{\text{Number of ways that event can occur}}{\text{All Possible Events}} $$

For example, if you are interested in getting to know the probability that out of a 52 card deck you are going to draw Ace of Hearts in a random draw, the probability of that is $ \frac{1}{52} $.

Why $ \frac{1}{52} $ you ask? Well, think about it. There are 52 cards present in the deck. All these cards are equally likely to get drawn from the deck when we draw randomly. Because we are interested in the likelihood of Ace of Hearts, we need to figure out in how many situations do we get this type of card when we draw. Well of course, the answer is 1 because there is only a single Ace of Hearts in the whole deck of 52 cards and so the probability becomes,

$$ P(\text{Ace of Hearts}) = \frac{\text{Number of ways I can get Ace of Hearts}}{\text{All Possible Outcomes of the random draw}} = \frac{1}{52} $$

Properties of Probability

There are a few properties of probability that you should always remember, as these are the fundamental rules governing any probability value, no matter how it's calculated or what type it is.

• Probability is always greater than or equal to Zero.
• Probability of an Impossible Event is Zero.
• Probability is always less than or equal to One.
• Probability of a Sure Event is One.
• If Probability of something happening is $ \text{P} $, then Probability of that thing NOT happening becomes $ 1 - \text{P} $

Terminologies in Probability

While learning probability, it's crucial that we understand a few terms that are used in probability a lot. These terms (or concepts) are key in dealing with different types of situations in which probability has to be computed. These terms include Experiments, Events, Sample Space, Unions, Intersections, Exhaustive Events, Independent Events, Mutually Exclusive Events, Complementary Events.

But before we dive into the technical definitions and understanding of these terms, let's define an example, that we will use as a reference in order to better grasp the intuition behind these terms. Let's say we've have a deck of 52 cards and we are drawing one card at a time, randomly from this deck.

Experiment and Event

In context of probability, an experiment is a process which produces events. So in our example of drawing cards from a deck of 52 cards drawing of a card is an experiment.

On the other hand, an event is a specific outcome of an experiment. So in our example, one particular event would be drawing a card that's an Ace of Clubs. Another event in our example could be drawing a card that's King of Hearts.

Under events, there is a special category of events called Elementary Events. Elementary events are special because they can't be decomposed. Now what do I mean by that? Well, in our example of drawing from the card deck, we can have an event like getting a card that's an Ace. But this is a de-composable event meaning I can further break it down in multiple events. This event is the combination of 4 events - Ace of Diamonds, Ace of Hearts, Ace of Clubs and Ace of Spades. Now let's take a look at the event drawing a card that is a King of Hearts. Well, this event can't be broken down any further. Why? Because you only have one King of Hearts in a deck of cards, you either get that or you don't. This is an Elementary Event.

Sample Space

In an experiment, a sample space is the collection of all possible outcomes of an experiment. In the card example, our sample space consists of 52 events (or outcomes).

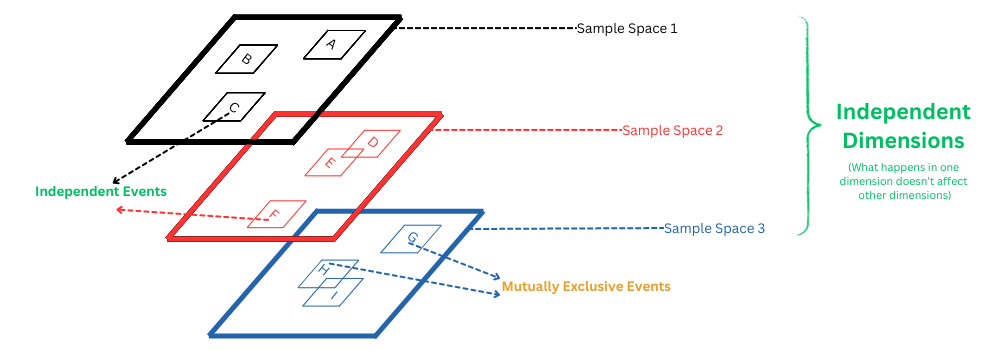
Independent Events

In probability, if two events are such that the occurrence of one event has no impact on another, then these events are called to be Independent events. If we think this from the perspective of our example, do you think the event of drawing an Ace from the deck and the event that it will rain tomorrow are related to each other in any way. Of course not, right. These two events are operating in a completely different sample space. They have no interdependence on each other whatsoever, and thus will be classified as Independent Events.

Mutually Exclusive Events

This one is really interesting as sometimes people get confused between Mutually Exclusive Events and Independent Events. I hope you are clear on what Independent Events are from the above section. Let's clearly understand what's Mutually Exclusive Events are and how are they fundamentally different from Independent Events.

If the occurrence of one event prohibits the occurrence of another event, then these events are called as Mutually Exclusive Events. So in our example, the event of drawing a Ace of Hearts and the event of drawing a king of spades would be an example of Mutually Exclusive Events. Why, you ask? Well, think about it, if I draw an Ace of Hearts then that means that I can't really have King of Spades because I have Ace of Hearts, obviously. In other situation, if one event is drawing an Ace and another event is drawing an Ace of Heart, then in that case these events are not mutually exclusive events, because occurrence of one event doesn't really mean in a definitive way that the other can't occur.

The reason why Mutually Exclusive Events are different then Independent Events is that in the case of Mutually Exclusive Events, the sample space of the events is the same. In other words, the mutually exclusive events are generated using the same experiment. On the other hand, the independent events are events that lie in independent sample spaces and have different experiments (processes) that generate those events.

Complementary Events

Another interesting category of events is the complementary events. Formally, if two events are such that the union of both the events is the entire sample space and intersection of both the events is null, then they are classified as Complementary Events. Too much, I know...😄.

Alright, let's breakdown what I said in above statement. Let's say you have two events A and B.

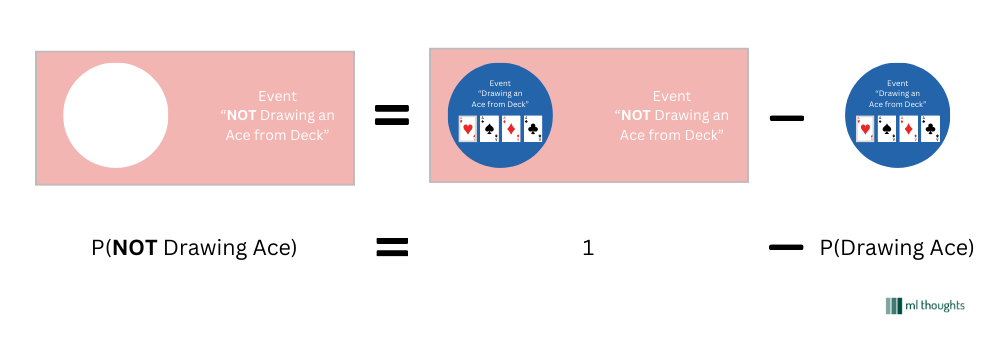
Event A: Drawing an Ace from the deck.
Event B: NOT Drawing an Ace from the deck.

In this situation, it's guaranteed that either Event A will happen or Event B will happen. This is because when we draw a card randomly, it will either be an Ace or it won't be. There's no third option possible. In other words, Event A and Event B combined covers the entire Sample Space of our experiment.

Now the other part of my statement above was regarding the intersection of the events, let's dissect that. If Event A happens then it's guaranteed that Event B won't happen and vice versa. In other words, Event A and Event B are also Mutually Exclusive Events.

So, in a nutshell when you have two events such as our events A and B which combined consists of the complete sample space and are also mutually exclusive events, then these events are known as Complementary Events.

Sum of the Probabilities of Complementary Events always add up to $ \text{1} $. This make sense as it is certain for one of them to occur. This can be seen in the figure below for our Deck of Cards example.

Alright, that's all for this post. In the next post in this series, we discuss about different types of probabilities.

Have any questions?
If you have any queries/doubts or anything you want to add, please mention in the comment section below. I try to answer queries and doubts on a regular basis so if you want any assistance regarding the material, do post it in the comments.

I'll see you in the next one.