Statistics 101 - Levels of Data

Alright, so this is a new series of posts in which I will focus on important statistical concepts from perspective of Data Science & Analytics applications, concepts which are generally applicable when working different types of Data Science projects. If you want to see all the posts under this series, just click on the "Statistics 101" tag above.

In this post we are going to start our statistical journey by discussing about different levels of data

Why to care about old boring statistics, at all?

However, before we start, since this is the first post in this series, I want to discuss a bit about the significance of statistics when working in a data science project or even better in relationship to machine learning.

Statistics is the grammar of science.
– Karl Pearson

I suppose truer words have never been spoken in context of Data Science and Machine Learning. Statistics, often overshadowed by the glamour and the "awe" factor of Deep Learning and Artificial Intelligence, remains crucial in delivering robust data science and machine learning based solutions.

There are many in the Data Science community, especially beginners, who want to directly jump to the coding bandwagon and a lot of the community do encourage them by stating the case that it's good for keeping up the motivation and that sooner some one case see some kind of result the better it is to keep them on the learning curve. Now don't get me wrong, I do agree with this point, however, the only issue here is that when this is being targeted towards beginners it's easy to understate the importance of statistics. Many beginners begin to see this above mentioned advice as a kind of approval to skip the details that are present in the underlying statistical or mathematical concepts being used in those programming packages.

Now, by no means I am advocating that you need to be a statistics expert or mathematics prodigy to work in the area of analytics and data science. However, that being said, it's paramount that you have an solid understanding of the fundamental statistical principles and concepts. If you won't, then as you progress in your data science journey, eventually you will start to feel that most of the times you aren't equipped with enough information to answer certain questions in order to progress in the project. And notice, I am using the frequently using the term Data Science and analytics, rather than Machine learning, that's no coincidence, it's by design. Many projects currently being worked in the Industry either have zero or very minimal dependence on a machine learning based solution. However, almost all of these projects rely on statistics, even if only at a basic level.

Another issue with not building your statistical skills as you progress through your analytics career, is that you won't be able to effectively and comprehensively parse the results of the analysis produced by the high-level frameworks being used in the project. For example, if you are using R and you are trying to build a simple model using regression analysis, for sure you will be able to build the model, but without understanding the underlying assumptions that come from a statistical perspective and without having a good grasp on concepts like hypothesis testing and confidence intervals, the true power of such models will be beyond your reach.

So in a nutshell, I would suggest to anyone who is just getting started in the field, to start with practical implementations and engage in as much coding as you like, however, just also keep in mind that eventually you need to start building your hard core skills like statistics, linear algebra and calculus etc. And the key thing to mention with these skills is that they take time to build, so it's better to engage them with in 80-20 ratio i.e. for every 80% of effort that you put into learning framekworks, tools, and building practical projects, put 20% of effort in learning the other part i.e. statistics, linear algebra, calculus, etc. In the short run, the affect of these might not be quickly visible but in long run they grant you a certain edge that only those realize who have it.

Alright, enough of me with this rant about why statistics and maths is so great and yada yada yada.... 😴

Levels of Data in Statistics

Let's get to the fun part. Let's talk about different types of data we use in statistics. Specifically, there are 4 types (or levels) in which you can classify data in statistics.

They are Nominal, Ordinal, Interval and Ratio. Let's discuss each of these one by one.

Nominal Data

This is the lowest level of data in statistics and contains the lowest amount of information. Let's see how.

Consider you have 3 dogs (Bruno, Marco and Polo) as pets and you want to get them vaccinated. Now you go to the website for animal welfare and fill up a form to get an appointment for your dogs. Now in this form, you are required to fill up how many pets you have. Once you do, it assigns Label "1" to refer to Bruno, "2" to refer to Marco and "3" to refer to Polo. Now looking at these labels, it's clear that these numbers are just for labelling purposes, however, they do not carry any value based information. In other words, Polo being referred to as "3" doesn't make it better than Bruno which is referred as "1".

This type of data which enables you to categorize or classify a variable, however, doesn't contain any further information is referred to as Nominal Data.

Ordinal Data

Next level of data after Nominal is what's called as "Ordinal" data. This type of data has a bit more information as compared to the nominal level as it has all the informational characterstics of nominal level and also has information about the order of the elements. Alright, so that came out a bit more complicated than I intended to make it. Let's try to understand it in simple terms.

Let's say you want to rate customer experience after they have purchased a product. After a few days of purchase, you send them a form which contains a rating of the product on a scale of 5, 5 representing the highest customer satisfaction and 1 representing the lowest. Now in this example, these labels for rating, doesn't just classify the customer satisfaction value, they also have certain order attached to them. For example, rating of 4 is higher than rating of 3 which is higher than rating of 2. This is what "Ordinal" data represents that the elements have order within them which can be used while dealing with this type of data.

Interval Data

Next, coming on to Interval data, we have all the properties of Nominal and Ordinal levels, and then some. Interval data in addition to having the ability to categorize and order the data also have the capability to measure intervals between different datapoints. To understand this ability, let's jump back to the ordinal data example.

In our example, while understanding Ordinal data we were discussing about the customer satisfaction ratings and we had the ratings on a scale of 5. It won't make much sense to subtract rating 4 from rating 5 as the difference between those doesn't really represent anything. The reason behind that is the interval (or distance) between rating 4 and rating 5 is not exactly equal to the interval (or distance) between rating 3 and rating 4. Now, this obviously shoudn't surprise us as these values of ratings are on a subjective level and the customer satisfaction represented by rating 3 is not exactly as less than rating 4 as rating 4 from rating 5. These are subjective values and thus having intervals between them doesn't make a sense from real world perspective.

In interval data, we have this exact possibility, the data points are numerical values and the intervals do exist between these data points.

Let's explore that further with an example of pH values. Most of us know about pH values through our chemistry lessons from school. pH in general is the measure of how acidic or basic a solution is. The value on a pH scale goes from 0 to 14, where 0 represents the most acidic solution and 14 represents the most basic solution. 7 is the pH value for a neutral solution which is neither acidic nor basic. pH values comes under the category of interval because of two specific reasons, which are as follows:

• There's no absolute zero. The value of pH "0" doesn't represent the absence of the acidic or basic nature. In fact, a zero ph value represents the most acidic solution.
• The ph values are equidistant. This means, that the difference between pH value of 5 and 6 is exactly equal to the difference between pH value of 6 and 7. In other words, when you move from pH value 5 to 6 and when you move from pH value of 6 to 7, the same level of decrease in the acidity will occur. If you remember, this wasn't the case with Ordinal data.

Another important point to note in case of interval data is that it is possible to have negative values in case of interval data since the value zero doesn't represent the absence of the measured entity. In our above pH example, this didn't happen as the scale is not designed for negative values, but just to make sure that you guys are aware of this fact, I thought I will mention it explicitly.

Ratio Data

And finally, we have the highest level of data measurement that we can, which is, Ratio level data. In addition to all the characterstics from Nominal, Ordinal and Interval levels, it contains a few more properties which makes it the highest level in terms of it's information holding capacity.

Before we proceed it's crucial to note that, similar to the Interval data, Ratio data also comprises of numerical values.

So, as we've already discussed, since ratio level data has the characterstics of all the previous levels of data, it has the ability to categorize data, order and take intervals between the data points. However, in addition it also has an absolute zero value. This is the value where the measured entity is absent. Hmmm, what does that mean 🤔? Well, it simply means, that if we take height as an example variable for our ratio data, we can clearly see that a height of "0" is no height at all. If something has a height of "0" that thing has no height at all. In other words, the height dimension is not present in that case. This is exactly what absence of the measured entity means.

Another important factor to understand, in case of ratio data, is that the concept of multiples and ratios is valid at this level. In other words, in case of ratio data, height of 6 cm is half of height of 12 cm. In other words, it can be stated that the height present in case of 12 cm is double of that what is present in case of 6cm.

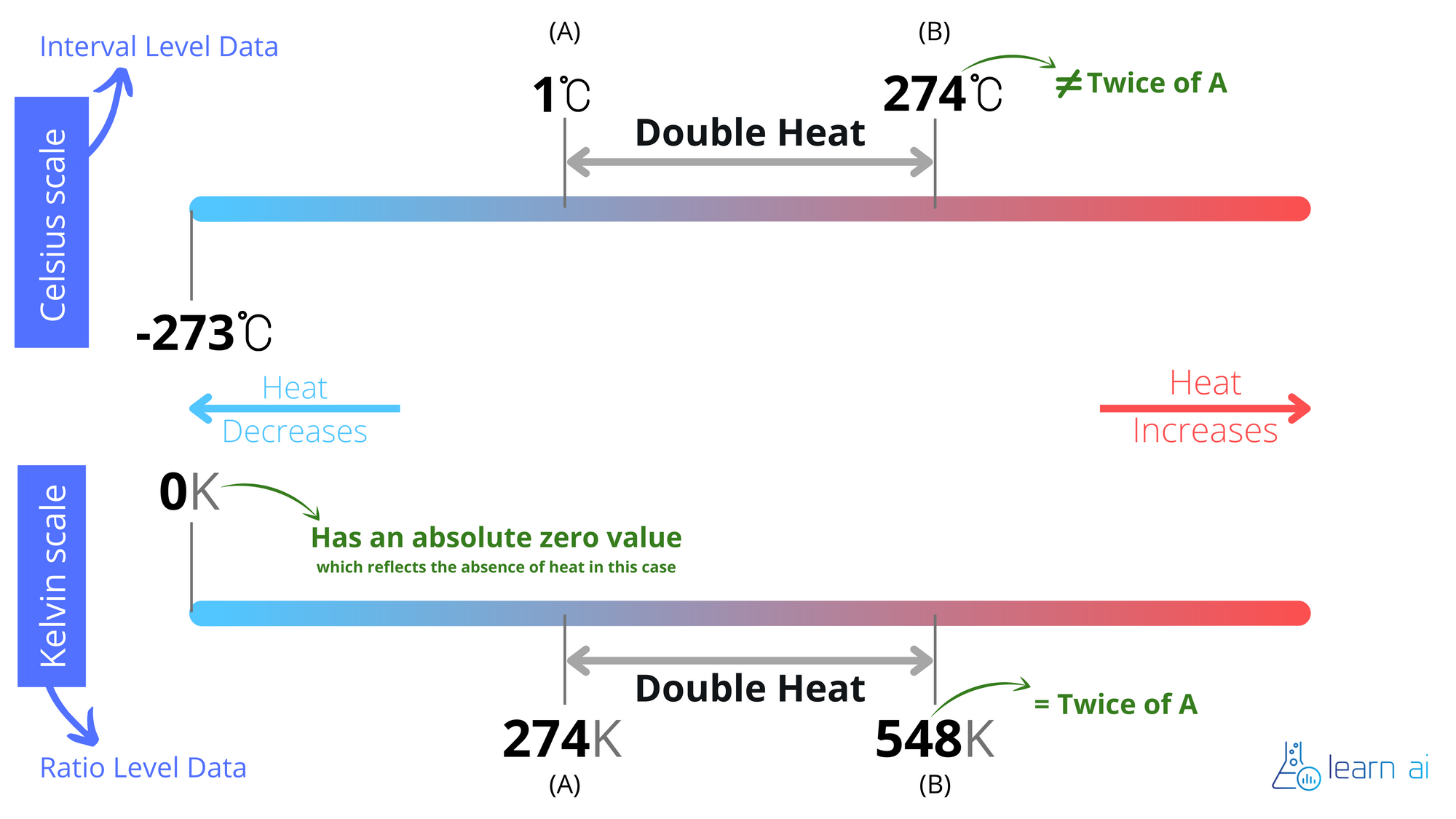
How's Ratio data different than Interval data?

Let's do this comparision through an example, that way it will be more clear. To make it completely clear, I've also included a visual illustration for this example below.

Temperature as we know, can be measured in degree celcius as well as in kelvin among other units. Now, temperature in kelvin is a ratio level data, however, temperature in celcius is an interval level data. Let's see how that affects the level of information that we have on both scales. In both cases, as temperature rises, the overall heat in the system is increasing and in general, temperature is ultimately a measurement of heat in the system. Now in the case of kelvin scale, the heat that is present at 548 K is double the heat that's present at 274K. However, when we translate these same temperature points on celcius scale, we can clearly see that 274 K translates to 1 degree celcius and 548 K translates to 274 degree celcius. So that means that on the celcius scale, to double the heat that's present at the temperature of 1 degree celcius, I would have to get to the temperature of 274 degree celcius, which obviously is not twice of 1 degree celcius.

Another interesting thing to note in this illustration is the fact that Kelvin scale, which operates at ratio level, does have an absolute zero, meaning that the zero value here represents the absence of heat in the system. Whereas, if you compare this, to the celcius scale, you will notice that the zero value here is an arbitrary value which doesn't really reflect the absence of measured entity and is just another value on the scale.

In a nutshell, levels of data in statistics represent the amount of information that's present in the data. Nominal data which is the lowest level represents lowest amount of information. Ratio data which is the highest level, represents the highest level of information. And, if you really think about it makes perfect sense, nominal data which has no information regarding the order or the interval of data points is obviously going to represent less value than ratio level data which contains all the characterstics of nominal, ordinal and interval data as well as some of the characterstics that are unique to ratio level itself.

This is all great, But what is Qualitative and Quantitative data?

I am sure, most of you must have heard at some point in time the terms - Qualititative Data and Quantitative Data. Amazing thing is, once you know the above-mentioned levels of data, understanding Qualitative and Quantitative data is fairly simple.

Nominal data and ordinal data are also referred to as Qualitative data. This is due to the fact that the variables or values represented by this type of data are more of a subjective nature and doesn't hold much mathematical value in terms of the operations that can be applied to these values.

On the other hand, Interval data and Ratio data, both make up the Quantitative data category.The reason these are called quantitative is that they mathematical properties embedded within them which make them suitable for most mathematical operations depending on the data level.